Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
기존의 연구들은 고정된 길이의 문맥만 처리할 수 있다는 한계를 갖고 있었다.
이런 문제점을 보완하기 위해 self attention network에 recurrence 구조를 도입한 Transformer-XL(extra long) 모델을 제안한다.
문맥을 여러 segment들로 나눈 후에 각각의 segment에 대해 hidden state를 계속 새로 계산하는 것이 아니라 이전 segment의 state를 메모리에 저장하고 재사용한다.
즉, segment들 사이에 recurrence 방식의 연결을 생성해 long-term dependency를 만들 수 있다.
또한, absolute가 아닌 relative positional encoding을 사용한다.
Model
Token들의 corpus \(x=(x_1,...,x_T)\)가 주어졌을 때, language modeling은 joint probability \(P(x)\)를 계산한다.
보통 \(P(x)\)는 AR 방식으로 \(P(x)=\Pi_t\:P(x_t\mid x_{<t})\)이다.
학습되는 NN은 문맥 \(x_{<t}\)를 고정된 크기의 hidden state로 encoding한다.
그리고 계산된 logit에 softmax를 적용해 다음 token들의 확률 분포를 얻는다.
Vanilla Transformer Language Models
Transformer나 self attention을 language model에 적용시키기 위해 중요한 문제는 임의의 길이의 문맥을 고정된 크기의 representation으로 표현하도록 transformer를 학습시키는 것이다.
메모리 같은 자원이 무한하다면 전체 문맥을 한번에 처리할 수 있겠지만, 실제로 그것은 불가능한 일이다.
단순한 방법은 전체 문맥을 segment들로 나누고 이전 segment로 부터의 문맥적인 정보를 무시하는 것이다.
이런 모델을 vanilla model 이라고 한다.
이러한 모델은 segment들 사이에 정보를 주고 받을 수 없다.
고정된 길이의 문맥을 사용하는 것은 2가지 치명적인 한계가 있다.
- segment의 길이 이상의 dependency를 생성할 수 없기 때문에 vanishing gradient의 관점에서 self attention의 장점을 최대로 활용할 수 없다.
- 하나의 sequence를 단순하게 여러 segment로 나누는 것은 context fragmentation 문제가 발생할 수 있다.
아래 그림은 segment의 길이가 4인 vanilla model의 학습 과정이다.
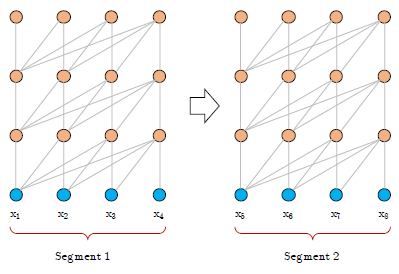
평가 과정에서는 매 step마다 학습시와 같은 길이의 segment를 사용한다.
다음 step으로 넘어가면서 segment도 한 position씩 움직인다.
하지만, 이 과정은 계산 비용이 매우 높다.
아래 그림은 vanilla model의 평가 과정이다.
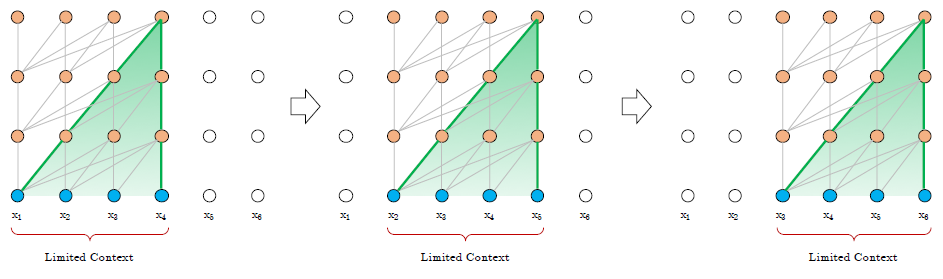
Segment Level Recurrence with State Reuse
고정된 길이를 사용하는 방법의 한계를 해결하기 위해 transformer 구조에 recurrence mechanism을 도입했다.
학습 과정에서 이전 segment에서 계산된 hidden state를 고정시키고 캐싱함으로써, 모델이 다음 segment를 처리할 때 캐싱된 정보를 사용해 문맥을 확장시킨다.
아래 그림은 이전 segment의 정보를 사용한 학습 과정을 보여준다.
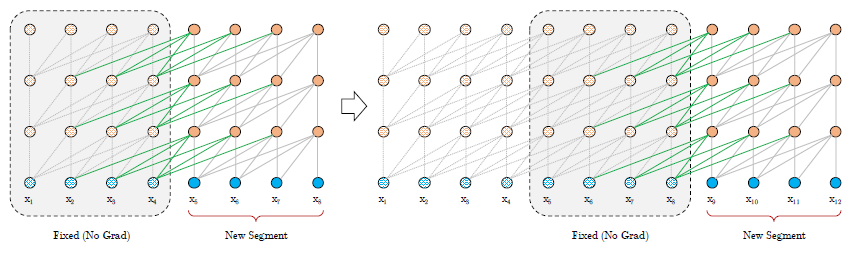
비록 이전 segment는 고정되어 더 이상 학습되지는 않지만, 모델이 history의 정보를 사용할 수 있게 하며 longer term dependency를 만들고 context fragmentation을 피할 수 있다.
길이가 \(L\)인 연속되는 두 segment \(s_\tau=[x_{\tau,1},...,x_{\tau,L}]\)와 \(s_{\tau+1}=[x_{\tau+1,1},...,x_{\tau+1,L}]\)이 있다고 할 때, segment \(s_\tau\)에서 만들어진 \(n\)번째 layer의 hidden state를 \(h_\tau^n\in \mathbb{R}^{L\times d}\)라고 표기한다. (\(d\)는 hidden dimension)
Segment \(s_{\tau+1}\)에서 만들어진 \(n\)번째 layer의 hidden state \(h_{\tau+1}^n\)은 아래와 같이 정의된다.
\[\tilde{h}_{\tau+1}^{n-1}=[SG(h_\tau^{n-1})\circ h_{\tau+1}^{n-1}]\] \[q_{\tau+1}^n,k_{\tau+1}^n,v_{\tau+1}^n=h_{\tau+1}^{n-1}W_q^T,\tilde{h}_{\tau+1}^{n-1}W_k^T,\tilde{h}_{\tau+1}^{n-1}W_v^T\] \[h_{\tau+1}^n=Transformer\,Layer(q_{\tau+1}^n,k_{\tau+1}^n,v_{\tau+1}^n)\]\(SG(\cdot)\)은 stop gradient, \(h_u\circ h_v\)는 concat을 의미한다.
일반적인 transformer와의 가장 중요한 차이는 key \(k_{\tau+1}^n\)과 value \(v_{\tau+1}^n\)가 확장된 문맥 \(\tilde{h}_{\tau+1}^{n-1}\)의 정보를 사용하고 \(h_{\tau}^{n-1}\)이 이전 segnment로 부터 캐싱된다는 점이다.
Recurrence 구조를 모든 연속되는 두 segment에 적용시키면 hidden state들에서 segment-level의 recurrence를 만들 수 있다.
여기서, \(h_{\tau+1}^n\)과 \(h_\tau^{n-1}\) 사이의 recurrent dependency는 같은 layer가 아닌 한 단계 아래의 layer와 연결된다.
즉, 일반적인 RNN language model과는 다르다고 할 수 있다.
최대로 가능한 dependency의 길이는 layer의 수와 segment의 길이가 늘어날 수록 증가한다.
또한, 마지막 truncated BPTT처럼 hidden state만 저장하는 것이 아니라 hidden state의 seqeunce를 저장한다.
아래 그림은 평가 과정을 보여준다.
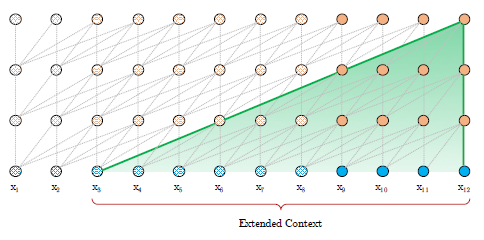
Recurrence 구조를 통해 긴 문맥과 fragmentation 문제를 해결할 수 있다는 점 외에도 segment의 결과를 재사용함으로써 모델의 평가 속도를 향상시킬 수 있다는 장점도 있다.
또한, GPU 메모리가 허용하는 만큼 여러 segment들을 재사용할 수 있다.
이전 segment들의 길이 \(M\)을 파라미터로 미리 정의하고 메모리 \(m_\tau^n\in \mathbb{R}^{M\times d}\)를 정의한다.
다시말해, GPU 메모리만 충분하다면 layer의 수와 segment의 길이를 크게 설정해 더 긴 문맥 정보를 활용할 수 있다.
Relative Positional Encoding
Hidden state들을 재사용할 때, 어떻게 positional information coherent를 보존할 것인지의 문제가 아직 남아있다.
일반적인 transformer에서 위치의 정보는 positional encoding의 집합 \(U\in \mathbb{R}^{L_{max}\times d}\)에서 얻는다.
여기서, \(U_i\)는 각 segment에서 \(i\)번째 위치를 의미하고 \(L_{max}\)는 모델에 입력할 수 있는 최대 길이이다.
Positional encoding을 recurrence 구조에 추가하면 아래와 같이 정리할 수 있다.
\[h_{\tau+1}=f(h_\tau,E_{S_{\tau+1}}+U_{1:L})\] \[h_{\tau}=f(h_{\tau-1},E_{S_{\tau}}+U_{1:L})\]\(E_{S_\tau}\in \mathbb{R}^{L\times d}\)는 sequence \(S_\tau\)의 word embedding이고, \(f\)는 transformation function을 의미한다.
주목할 점은 \(h_{\tau+1}\)과 \(h_\tau\) 모두 같은 positional encoding \(U_{1:L}\)을 사용한다는 것이다.
즉, \(j=1,...,L\)인 \(j\)에 대해 \(x_{\tau,j}\)와 \(x_{\tau+1,j}\)의 위치 정보를 구분할 수 없다.
이런 단점을 해결하기 위해, relative positional encoding을 사용한다.
이 방법은 모델에게 어떤 위치에 집중해야 하는지에 대한 정보를 준다.
또한, 초기 embedding에 bias를 정적으로 통합시키는 것이 아닌, 각 layer의 attention score에 동일한 정보를 주입할 수 있다.
Relative한 관점에서 일시적인 bias를 정의하는 것이 보다 직관적이고 일반적이다.
예를 들면, query vector \(q_{\tau,i}\)가 key vector들 \(k_{\tau,\leq i}\)들에 관여할 때, 각각 key vector들의 absolute position을 알 필요가 없다.
단지, relative position인 \(i-j\)만 알면 된다.
Relative positional encoding의 집합을 만들면, \(R\in \mathbb{R}^{L_{max}\times d}\)를 만들 수 있다.
여기서, \(R_i\)는 두 position 사이의 거리가 \(i\)일 때의 relative encoding이다.
Relative encoding을 사용함으로써, \(x_{\tau,j}\)와 \(x_{\tau+1,j}\)를 구분할 수 있다.
일반적인 transformer에서는 같은 segment의 query \(q_i\)와 key \(k_j\)사이의 attention score는 아래와 같이 계산한다.
\[A_{i,j}^{abs}=E_{x_i}^TW_q^TW_kE_{x_j}+E_{x_i}^TW_q^TW_kU_j+U_i^TW_q^TW_kE_{x_j}+U_i^TW_q^TW_kU_j\]Relative positional encoding을 적용하면 아래와 같이 바꿀 수 있다.
\[A_{i,j}^{rel}=E_{x_i}^TW_q^TW_{k,E}E_{x_j}+E_{x_i}^TW_q^TW_{k,R}R_{i-j}+u^TW_{k,E}E_{x_j}+v^TW_{k,R}R_{i-j}\]먼저, \(U_j\)를 \(R_{i-j}\)로 바꿨다.
두번째로, \(U_i^TW_q^T\)를 학습 가능한 파라미터 \(u\in\mathbb{R}^d\)와 \(v\in\mathbb{R}^d\)로 바꿨다. 여기서, query vector는 query의 위치에 관계 없이 항상 같아야 한다.
마지막으로, content based key vector와 location based key vector를 독립적으로 만들기 위해 \(W_k\)를 분리시켰다.
하나의 attention head와 \(N\)개의 layer로 이루어진 Transformer-XL의 계산 과정은 아래와 같이 나타낼 수 있다.
\[\tilde{h}_\tau^{n-1}=[SG(m_\tau^{n-1})\circ h_\tau^{n-1}]\] \[q_{\tau}^n,k_{\tau}^n,v_{\tau}^n=h_{\tau}^{n-1}{W_q^n}^T,\tilde{h}_{\tau}^{n-1}{W_{k,E}^n}^T,\tilde{h}_{\tau}^{n-1}{W_v^n}^T\] \[A_{\tau,i,j}^n={q_{\tau,i}^{n}}^Tk_{\tau,j}^n+{q_{\tau,i}^{n}}^TW_{k,R}^nR_{i-j}+u^Tk_{\tau,j}+v^TW_{k,R}^nR_{i-j}\] \[a_\tau^n=Masked\,Softmax(A_\tau^n)v_\tau^n\] \[o_\tau^n=LayerNorm(Linear(a_\tau^n)+h_\tau^{n-1})\] \[h_\tau^n=Positionwise\,Feed\,Forward(o_\tau^n)\]여기서, \(n=1,...,N\)이고 \(h_\tau^0=E_{s_\tau}\), 즉, word embedding sequence이다.
\(A\)를 계산하기 위해 naive한 방법을 사용한다면 모든 \((i,j)\) 쌍에 대해 계산을 해야하고 이는 굉장히 비효율적이다.
하지만, \(i-j\)는 0부터 sequence length 까지의 범위이기 때문에 계산량을 효율적으로 줄일 수 있다.
논문 링크
ACL 2019
Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

Leave a comment