Worker Model for Crowdsourcing
1. 개발 도구
-
Python3
-
Matlab
2. 데이터
대학 과목의 프로젝트로 주어진 matrix 형태의 crowdsourcing 데이터를 사용 (데이터는 공개하지 않음)
여러 worker들이 여러 binary classification task들에 대해 labeling한 결과를 Matlab matrix로 표현
SYN dataset
각 worker들에 할당된 task들의 수 \(r\)을 \([1,3,5,7,9,11,13]\)으로 증가시키며 각각의 \(r\)에 대해 worker들이 task들에 부여한 label들을 matrix로 표현한 데이터
SIM dataset
각 task들에 할당된 worker들의 수 \(l\)을 \([1,5,10,15,20,25]\)으로 증가시키며 각각의 \(l\)에 대해 worker들이 task들에 부여한 label들을 matrix로 표현한 데이터
데이터 처리
Matlab으로 주어진 데이터들을 Python3에서 제공하는 Scipy를 사용하여 읽음
Matlab 데이터에서 각 worker들과 task들의 연결 상태, 각 worker들이 task들에 부여한 label 등을 Python 변수로 파싱
4. 모델
같은 데이터들에 대해서 MV, BP, EM 모델을 구현하여 결과를 비교
MV(Majority Voting)
Worker Model 중에서 가장 단순한 모델로, 각 task들에 대해 할당된 worker들이 부여한 label들을 확인하여 다수의 worker들이 결정한 label을 해당 task의 true label로 판정
MV 모델은 worker들의 reliability를 고려하지 않고 모든 worker를 동일하게 취급하기 때문에 정확도가 떨어지는 단점이 존재
BP(Belief Propagation)
Worker와 task들의 관계를 worker를 factor로, task를 variable로 하는 factor graph로 간주하여 iteration마다 message를 전달하여 worker들의 reliability와 task의 label을 추정하는 모델
Prior가 되는 worker들의 reliability는 beta 분포를 따른다고 가정
\(s\): 각 task들의 label을 의미하는 variable
\(A\): worker들이 task에 부여한 label matrix
\(p\): worker들의 reliability
\(u\): 각 worker들을 의미하는 variable
\(W\): worker의 집합
\(N_u\): \(u\)에 할당된 task들의 집합
\(r_u\): \(u\)에게 할당된 task의 수
\(c_u\): \(u\)가 정확하게 label을 부여한 task 수
\(f_u(s_{N_u})\): \(u\)의 \(N_u\)들에 대한 factor
\(\pi(p_u)\): prior \(p_u\)의 분포
라고 하면 다음과 같이 posterior를 정의 가능
\[\large\mathbb{P}[s\mid A]=\int\mathbb{P}[s,p\mid A]dp\\ \large\propto\Pi_{u\in W}\underbrace{\int_0^1\pi(p_u)\cdot p_u^{c_u}(1-p_u)^{r_u-c_u}dp_u}_{\Large :=f_u(s_{N_u})}\]여기서, \(f_u(s_{N_u})\)를 다음과 같이 정의할 수 있음
\[\large f_u({s_{N_u}}):=\mathbb{E}_{p_u}[p_u^{c_u}(1-p_u)^{r_u-c_u}]\]Prior \(p_u\)가 beta(\(\alpha,beta\)) 분포를 따를 때, \(f_u(s_{N_u})\)는 아래과 같은 값을 가짐
\[\large f_u(s_{N_u})=\frac{\Gamma(\alpha+\beta)\Gamma(\alpha+c_u)\Gamma(\beta+r_u-c_u)}{\Gamma(\alpha)\Gamma(\beta)\Gamma(\alpha+\beta+r_u)}\]\(i\): 각 task들을 의미하는 variable
\(s_i\): \(i\)의 label을 의미하는 variable, binary classification task이므로 \(s_i\in\{1,2\}\)
\(M_i\): \(i\)에 연결된 worker들의 집합
\(m_{i\rightarrow u}^{t}(s_i)\): time step \(t\)에서 \(i\)가 \(u\)에게 전달하는 \(s_i\)에 대한 message
\(b_i^t(s_i)\): time step \(t\)에서 \(i\)의 \(s_i\)에 대한 확률 또는 신뢰도
라고 하면 다음과 같이 매 itereration마다 worker와 task가 서로 message를 전달하며 worker의 reliability와 task의 label \(s_i\)를 update 할 수 있음
\[\large m_{i\rightarrow u}^{t+1}(s_i)\propto\Pi_{v\in M_i\text{\\}\{u\}}m_{v\rightarrow i}^t(s_i)\]\(i\)에서 \(u\)에게 message를 전달, 즉, \(u\)의 reliability를 update
이 message 값은 이전 time step \(t\)에서 \(i\)가 연결된 worker들에게 받은 message 값들의 product로 추정
이 때, target worker인 \(u\)로부터 받은 message는 product에서 제외
\[\large m_{u\rightarrow i}^{t+1}(s_i)\propto\sum_{s_{N_u\text{\\}\{i\}}}f_u(s_{N_u})\Pi_{j\in N_u\text{\\}\{i\}}m_{j\rightarrow u}^{t+1}(s_j)\]\(u\)에서 \(i\)에게 message를 전달, 즉, \(i\)의 label \(s_i\)를 update
이 message 값은 time step \(t+1\)에서 \(u\)가 연결된 task들에게 받은 message와 factor의 곱의 sum으로 추정
이 때, target task인 \(i\)로부터 받은 message는 sum에서 제외
Naive한 BP 모델에서 binary task에 대해 위의 식을 계산하기 위해서는 \(\large 2\times 2^{\mid N_u\text{\\}\{i\}\mid}\)번의 계산이 필요하기 때문에 time complexity가 매우 높음
\[\large b_i^{t+1}(s_i)\propto\Pi_{u\in M_i}m_{u\rightarrow i}^{t+1}(s_i)\]\(i\)의 belief를 update, 즉, \(i\)의 label \(s_i\)들이 어느정도의 신뢰성이 있는지를 추정
이 belief 값은 time step \(t+1\)에서 \(i\)가 연결된 worker들에게 받은 message 값들의 product로 추정
\[\large \hat{s}_i^{(k)}=argmax_{s_i}b_i^k(s_i)\]\(k\)번의 iteration 후의 task \(i\)의 새로운 label \(\hat{s}_i\)는 \(i\)의 belief \(b_i^k(s_i)\)를 최대화하는 \(s_i\)로 update
EM(Expectation Maximization)
\(p_u\)가 beta(\(\alpha,\beta\))를 따를 때, 아래와 같이 E-step과 M-step을 유도 가능
E-step
E-step에서는 parameter \(p_u\)를 고정시키고 \(s_i\)의 확률을 추정
\[\large \mathbb{P}(s_i\mid A,p)\propto\Pi_{u\in M_i}\:p_u^{1[A_{iu}=s_i]}(1-p_u)^{1[A_{iu}\neq s_i]}\\ 1[state]=\begin{cases}1&\text{, if state is ture} \\0&\text{, else}\end{cases}\]\(i\)의 새로운 label \(\hat{s}_i\)는 아래와 같이 추정
\[\large \hat{s}_i(A,p)=argmax_{s_i}\Pi_{u\in W_i}\: \mathbb{P}(s_i\mid A,p)\]M-step
M-step에서는 E-step에서 계산한 \(s_i\)의 확률을 고정시키고 새로운 worker의 reliability \(\hat{p}_u\)를 추정
\[\large \hat{p}_u=\frac{\sum_{i\in N_u}\mathbb{P}(A_{iu})+\alpha-1}{\mid N_u\mid+\alpha+\beta-2}\\ \mathbb{P}(A_{iu})=\begin{cases}\mathbb{P}(s_i=1)&\text{, if }A_{iu}=1\\\mathbb{P}(s_i=2)&\text{, if }A_{iu}=2\end{cases}\]E-step과 M-step을 반복하며 \(s_i\)를 update
(Variational Inference for Crowdsourcing 논문 참고)
5. 결과
BP와 EM 모델은 최대 iteration은 100번으로 지정
\(\mathbb{P}(s_i)\)의 변화량이 1e-5 이하인 경우 convergence가 됐다고 판단하여 iteration을 종료
Worker Model가 추정한 \(s\)와 dataset의 true label과 비교하여 error rate를 측정
SYN dataset
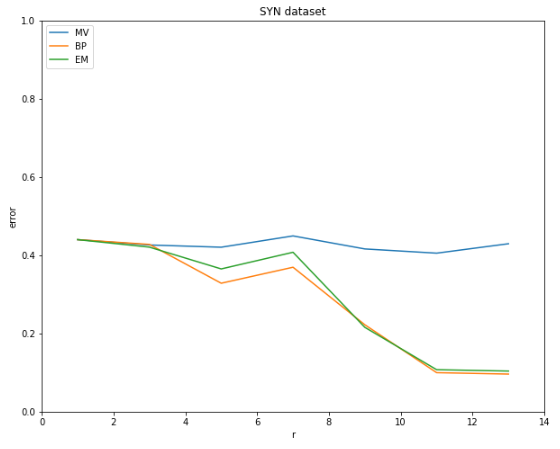
\(r\)이 증가해도 MV 모델의 성능은 향상되지 않는 것을 확인
즉, 한명의 worker가 더 많은 task를 할당받아도 각 task들에 대한 정확도는 향상되지 않음
BP와 EM 모델에서는 \(r\)이 증가할수록 성능이 향상되는 것을 확인
즉, 한명의 worker가 더 많은 task를 할당받으면 해당 worker의 reliability를 더 정확하게 판단할 수 있기 때문에 각 task들에 대한 정확도가 향상
SIM dataset
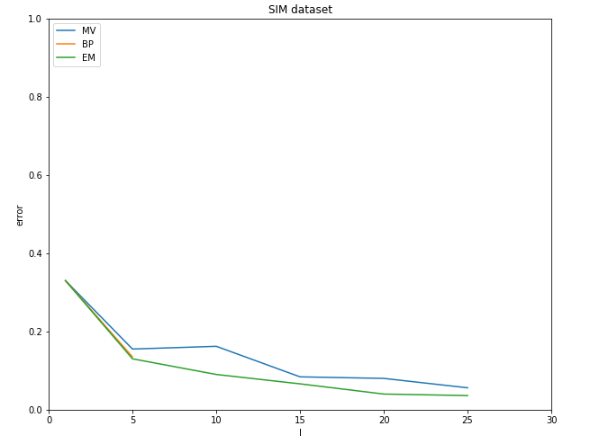
BP 모델을 naive하게 구현하여 worker에 할당된 task 수가 많아지면 시간이 오래걸려 BP 모델에 대해서는 \(l\)이 \([1,5]\)일 때만 측정
\(l\)이 증가하면 MV를 포함해 모든 모델의 성능이 향상되는 것을 확인
단순한 MV 모델에서도 하나의 task에 할당된 worker의 수가 많아지면 정확도가 향상되는 것을 확인

Leave a comment