t-SNE
지난번 포스팅에 이어 차원축소와 시각화에 많이 사용되는 t-SNE에 대해 알아보고자 한다.
SNE(Stochastic Neighbor Embedding)
SNE는 고차원의 데이터 \(X\)에서 이웃한 데이터간의 거리를 최대한 보존하면서 저차원으로 축소된 데이터 \(Y\)를 만드는 알고리즘이다.
데이터간의 거리를 확률적으로 표현하기 때문에 stochastic이라는 이름이 붙는다.
\(X\)의 \(i\)번째 데이터 \(x_i\)가 주어졌을 때 \(j\)번째 데이터 \(x_j\)가 이웃으로 선택될 확률을 \(p_{j\mid i}\), \(Y\)의 \(i\)번째 데이터 \(y_i\)가 주어졌을 때 \(j\)번째 데이터 \(y_j\)가 이웃으로 선택될 확률을 \(q_{j\mid i}\)라고 하면 \(p_{j\mid i}\)와 \(q_{j\mid i}\)는 아래와 같다.
\[p_{j|i} = \frac{e^{-\frac{|x_i - x_j|^2}{2\sigma_i ^2}}}{\sum_k{e^{-\frac{|x_i - x_k|^2}{2\sigma_i ^2}}}}, \sigma_i : hyper parmeter\] \[q_{j|i} = \frac{e^{-{|y_i - y_j|^2}}}{\sum_k{e^{-{|y_i - y_k|^2}}}}\]여기서 SNE의 목표는 \(p_{j\mid i}\)와 \(q_{j\mid i}\)의 차이를 최소화하는 것이다.
즉, \(p\)와 \(q\)의 분포를 최대한 비슷하게 만들어야 한다.
이때, KL divergence를 사용한다.
Loss는 아래와 같다.
\[Loss = \sum_i{KL(P_i || Q_i)} = \sum_i{\sum_j{p_{j|i}log\frac{p_{j|i}}{q_{j|i}}}}\]SNE의 단점은 Loss의 최적화가 쉽지 않고 crowding problem이 존재한다.
Crowding problem이란 데이터가 일정 부분에 밀집하게 되는 문제인데 SNE는 가우시안 분포를 전제로 하기 때문에 데이터들이 중심에 많이 분포하게 된다.
즉, j번째 데이터가 i번째 데이터에서 적당히 멀리 떨어져 있을 때와 아주 멀리 떨어져 있을 때의 확률의 차이가 크지 않아 클러스터링의 문제가 발생한다.
t-SNE
t-SNE는 SNE의 단점을 개선하기 위해 대칭적인 SNE를 사용한다.
t-SNE에서는 \(p_{j\mid i}\)가 아닌 \(p_{ij}\)를 사용하고 \(p_{ij}\)는 아래와 같다.
\[p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}, n : 데이터 수\]또한 crowding problem을 해결하기 위해 Q의 분포로 가우시안 분포가 아닌 t 분포를 사용한다.
\[q_{ij} = \frac{(1+|y_i -y_j|^2)^{-1}}{\sum_{k\neq l}{(1+|y_k -y_l|^2)^{-1}}}\]t-SNE의 Loss는 아래와 같다.
\[Loss = \sum_i{KL(P_i||Q_i)} = \sum_i{\sum_j{p_{ij}log\frac{p_{ij}}{q_{ij}}}} = \sum_i{\sum_j{p_{ij}\log{p_{ij}}-p_{ij}\log{q_{ij}}}}\]t-SNE는 위의 Loss를 최소화하는 방향으로 학습되어 데이터간 거리가 큰 것은 유사하지 않은 것으로, 데이터간 거리가 작은 것은 유사한 것으로 클러스터링할 수 있다.
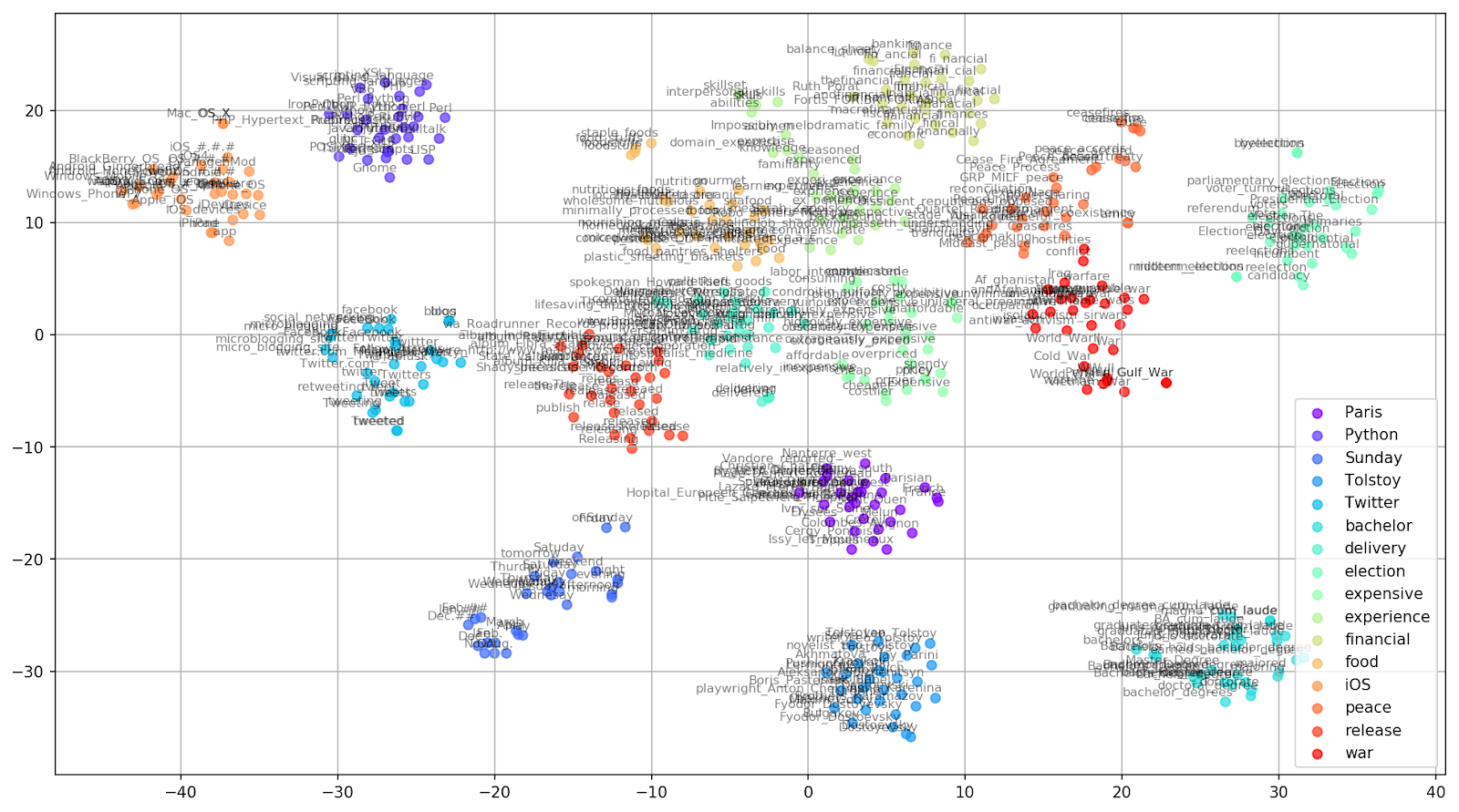
t-SNE가 사용되는 대표적인 예는 아래처럼 고차원 벡터인 단어 데이터들의 차원을 축소해 시각화하는 것이다.

Leave a comment