SVD(Singular Value Decomposition)
지난번 포스팅에 이어 차원축소에 많이 사용되는 SVD에 대해 알아보고자 한다.
SVD(Singular Value Decomposition)
SVD, 또는 특이값 분해는 고유값 분해와는 다르게 정방행렬이 아닌 행렬에도 적용가능하다.
\(m\times n\)인 행렬 \(A\)에 대해 SVD는 아래와 같이 적용한다.
\[A = U\sum V^T\]\(U : m\times m\)인 직교행렬, \(AA^T = U(\sum \sum ^T)U^T\), 즉, \(U\)는 열벡터가 \(AA^T\)의 고유벡터를 정규화한 값인 행렬이다.
\(\sum : m\times n\)인 대각 행렬
\(V^T : n\times n\)인 직교행렬, \(A^T A = V(\sum ^T \sum)V^T\), 즉, \(V^T\)는 열벡터가 \(A^T A\)의 고유벡터를 정규화한 값인 행렬의 전치행렬이다.
여기서 \(\sum\)은 \(AA^T\) 또는 \(A^T A\)를 고유값 분해해서 얻어지는 고유값들의 제곱근을 원소로 갖는 대각행렬이며 그 대각원소들을 행렬 A의 특이값(Singular Value)라고 한다.
기하학적 의미
행렬은 선형변환으로도 볼 수 있다.
예를들어, \(x' = Ax\)처럼 행렬 \(A\)가 벡터 \(x\)를 \(x'\)로 변환시킨다고 볼 수 있다.
이 때, \(A\)가 직교행렬이면 \(x'\)는 \(x\)의 회전변환된 결과이고 \(A\)가 대각행렬이면 \(x'\)는 \(x\)의 스케일변환된 결과이다.
즉, SVD는 아래와 같은 기하학적 의미를 갖는다.
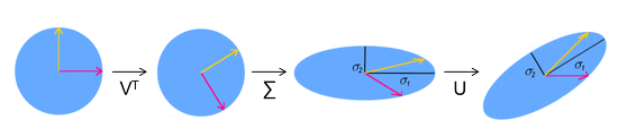
차원 축소
SVD에는 여러 형태가 있다.
일반적인 full SVD는 아래와 같다.
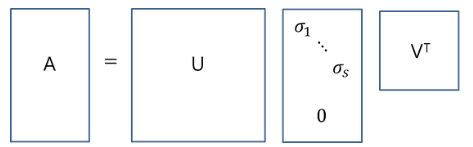
\(\sum\)을 \(s\times s\)으로 줄이면 아래와 같이 thin SVD를 만들 수 있다. (\(s=n\))
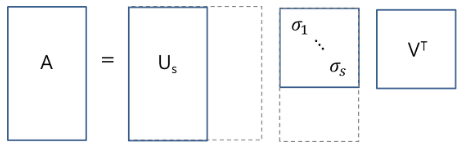
특이값 중 0인 값들을 제거해 \(r\)개의 특이값만 남기면 아래와 같이 compact SVD를 만들 수 있다.
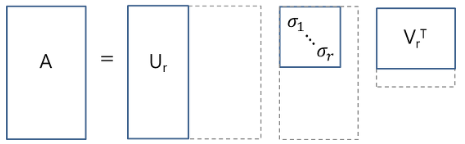
여기서 \(r\)개의 특이값 중 \(t\)개의 특이값만 사용해 아래와 같이 truncated SVD를 만들 수 있다.
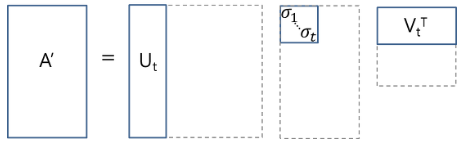
위와 같은 방법으로 n개의 singular value를 t개로 줄일 수 있다. 즉, n차원을 t차원으로 축소할 수 있다.
위의 그림에서 \(U\sum V^T\)로 \(A\)에 근사한 \(m\times n\)인 행렬 \(A'\)를 얻을 수 있다.
\(U\sum\)을 하면 \(m\times n\)이 아닌 \(m\times t\)의 행렬을 얻을 수 있다.
이러한 차원 축소를 추천 시스템에도 이용할 수 있다.
행렬 \(A\)가 m명의 사용자들의 n개의 영화에 대한 평점행렬이라고 하자.
여기서 모든 사용자들이 모든 영화를 감상한 것은 아니기 때문에 행렬에 빈 값이 존재할 것이다.
즉, 그 빈 값을 예측할 수 있다면 해당 사용자가 아직 감상하지 않은 영화에 대한 평점을 예측할 수 있고 높은 평점이 예측되면 그 영화를 사용자에게 추천할 수 있다.
먼저, \(A\)에서 빈 값은 각각 사용자가 다른 영화들에 준 평점의 평균 값으로 초기화한다.
\(A\)를 위의 그림과 같이 compact SVD나 truncated SVD형태로 만들면 평점행렬(\(A\))를 차원이 축소된 사용자행렬(\(U\)), 가중치행렬(\(\sum\)) 그리고 영화행렬(\(V^T\))로 나눌 수 있다.
다시 \(U\sum V^T\)를 하면 $A$에 근사한 $A’$를 만들 수 있다.
이 \(A'\)가 \(A\)에 가까워지도록 Gradient Descent 알고리즘으로 행렬 \(U\), \(\sum\), \(V\)를 학습한다.
학습이 완료되면 \(A\)에는 관측되지 않은 값을 \(A'\)를 통해 예측할 수 있다.
이처럼 SVD를 사용하면 \(U\)(사용자행렬)과 \(V^T\)(영화행렬)을 축소해서 처리량을 줄일 수 있고 근사 행렬 \(A'\)를 만들어 결측값을 예측할 수 있다.

Leave a comment