PCA(Principal Component Analysis)
이번 포스팅에서는 차원축소에 많이 사용되는 PCA에 대해 알아보고자 한다.
PCA(Principal Component Analysis)
PCA, 또는 주성분 분석은 데이터들의 분산(Variance) 정도를 최대한 보존하면서 서로 직교하는 축들을 찾는 것에서부터 시작된다.
즉, 데이터의 분포를 가장 잘 나타낼 수 있도록 새로운 축들을 찾아야 한다.
이 축들을 찾기 위해서는 먼저 데이터 행렬 X의 공분산행렬(Covariance Matrix), C를 구해야 한다.
X가 각 평균이 0인 d개의 feature를 갖는 n개의 점으로 이루어져 있다고 하면 공분산행렬 C는 아래와 같이 구할 수 있다.
\[C = \frac{X^T X}{n}\]
공분산행렬 C는 \(d\times d\)인 정방행렬이자 대칭행렬이 될 것이다.
열벡터가 공분산행렬 C의 고유벡터인 행렬을 V, 대각성분이 C의 고유값이고 대각 성분을 제외한 값은 0인 행렬을 \(\sum\)이라고 할 때, 아래와 같이 정리할 수 있다.
\[CV = V\sum\] \[C = V\sum V^-1\]여기서 C는 대칭행렬이기 때문에 \(C = C^T\)이고 \(V\sum V^-1 = (V^-1)^T\sum V^T\)임을 알 수 있다.
즉, \(V^-1 = V^T\)이고 \(V^T V = I\)이기 때문에 C의 고유벡터들이 서로 직교함을 확인할 수 있다.
공분산행렬 C에서 고유벡터-고유값 쌍은 총 d개를 구할 수 있고 이를 고유값에 대해 내림 차순으로 정렬하면 d개의 고유값 \(\lambda_1, \lambda_2, ..., \lambda_d\)와 d개의 고유벡터 \(v_1, v_2, ..., v_d\)를 구할 수 있다.
여기서 고유벡터 v들은 데이터의 분포를 나타내는 방향들을 의미하고 고유값은 그 방향이 데이터를 얼마나 잘 설명하는지의 정도를 의미한다고 볼 수 있다.
다시말하면 \(\lambda_1\)이 가장 크기 때문에 \(v_1\) 방향으로 데이터가 가장 잘 분산되어 있다고 볼 수 있다.
이 고유벡터 v중에서 k개를 골라 X에서 차원이 축소된 데이터 Z를 만들 수 있다.
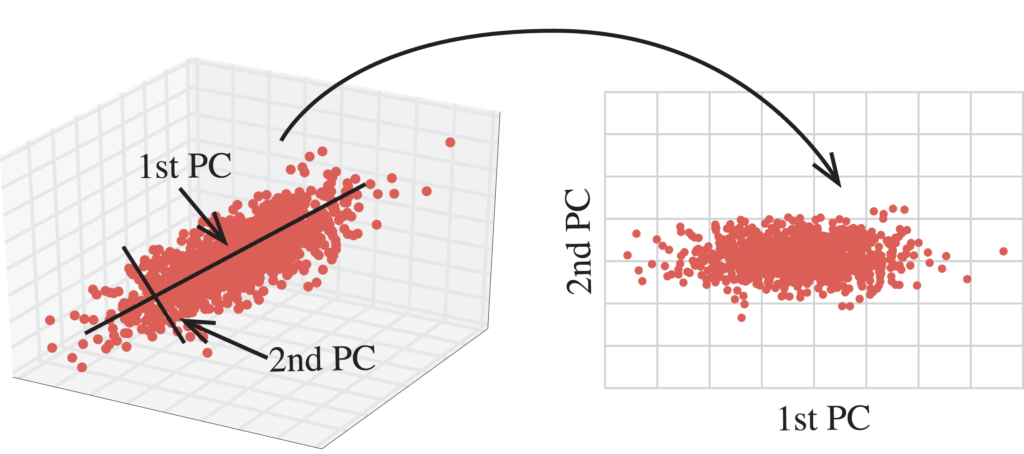
\[z_1=Xv_1, z_2=Xv_2, ..., z_k=Xv_k\] \[Z=[z_1 z_2 ... z_k]\]PCA를 사용해 고차원의 데이터를 저차원으로 축소하면 아래와 같이 시각적으로 데이터의 분포를 확인할 수 있다.

Leave a comment