Hierarchical Recurrent Attention Network for Response Generation
챗봇 시스템은 크게 특정한 task에만 한정된 task oriented 챗봇과 특정 task에 제한되지 않고 자연스럽고 사람처럼 대화하는 non task oriented 챗봇, 두 종류가 있다.
대부분의 챗봇을 만들 때는 많은 양의 message-response 쌍의 데이터로 encoder-decoder 형태의 response generation 모델을 학습시킨다.
하지만 이러한 모델들은 대화의 history를 무시하고, 이는 실제 사람들의 대화와는 상당히 다르다고 할 수 있다.
이런 문제점을 해결하기 위해 multi turn 챗봇 시스템들이 연구되고 있다.
본 연구에서는 open domain에 대해 multi turn 챗봇 시스템을 연구했으며 response와 그 context를 통해 모델을 학습시켰다.
여기서, context는 하나의 message와 그 이전 turn들의 utterance들을 의미한다.
모델은 context를 입력으로 받으면 다음 turn의 response를 생성한다.
Multi turn의 대화를 위해서는 모델이 전체 context를 고려해 response를 만들어야 한다.
이러한 task는 2가지 관점에서 어려움이 있다.
-
context는 utterance들로 이루어져 있고, utterance는 word들로 이루어진다.
즉, 대화의 context는 hierachical한 구조이며 이는 word들, utterance들 사이의 2종류의 sequential한 관계를 갖는다.
-
context는 모든 부분들이 response를 생성함에 있어 같은 중요도를 갖지 않는다.
다시말해, word들과 utterance들은 각각 다른 정보와 중요도를 갖는다.
아래 그림은 context와 response의 예시이다.

위의 예시에서는 \(u_1\)과 \(u_4\)가 response를 생성함에 있어 중요한 정보를 가지고 있다.
Word와 utterance들의 중요도를 신경쓰지 않고 hierachical한 구조만 고려하면 Are you a man or woman? 과 같은 부적절한 response를 생성하게 된다.
따라서, 본 연구에서는 word와 utterance의 중요도와 hierachical한 구조를 같이 고려하는 Hierachical Recurrent Attention Network(HRAN)을 제안한다.
HRAN은 hierachical한 구조에서 build된다.
HRAN의 첫번째 layer에서는 word level의 RNN이 각각의 utterance들을 hidden vector의 sequence로 encoding한다.
Response에서 각각의 word를 생성할 때는, word level의 attention이 각각의 vector들에 weight를 할당하고 그 vector들의 linear combination을 통해 하나의 utterance vector를 생성한다.
즉, 중요한 utterance는 response의 utterance를 생성할 때, 더 많은 관여를 하게 된다.
두번째 layer에서는 word level RNN이 만든 utterance vector들은 utterance level의 RNN에 입력되어 context의 hidden representation을 생성한다.
HRAN에서 word level의 attention은 decoder와 utterance level RNN에 dependency를 가진다.
따라서, 현재까지 생성된 response와 context의 정보를 통해 word level의 attention이 utterance들에서 중요한 부분을 선택할 수 있다.
세번째 layer에서는 utterance attention이 utterance들의 sequence에서 중요한 utterance에 가중치를 부여하고 sequence를 하나의 context vector로 만든다.
마지막 layer에서는 decoder가 context vector를 입력받아 response의 word를 생성한다.
Problem Formalization
데이터 셋 \(\mathbb{D}=\{(U_i,Y_i)\}_{i=1}^N\) 에 대해, response \(Y_i=(y_{i,1},...,y_{i,T_i})\) , context \(U_i=(u_{i,1},...,u_{i,m_i})\) 이고, \(y_{i,j}\)는 \(j\) 번째 word, \(u_{i,m_i}\)는 message, \((u_{i,1},...,u_{i,m_i-1})\)은 이전 turn들의 utterance이다.
본 연구에서 \(m_i \geq2\)로 조건을 뒀고, 그러므로 각각의 context는 대화의 history로 적어도 하나의 utterance를 갖는다.
\(u_{i,j}=(w_{i,j,1},...,w_{i,j,T_{i,j}})\)이고 \(w_{i,j,k}\)는 \(k\)번째 word이다.
데이터 셋 \(\mathbb{D}\) 로 부터 \(p(y_1,...y_T\mid U)\)를 계산한다.
다시말하면, 대화의 context \(U\)가 주어졌을 때, response \(Y=(y_1,...y_T)\)를 생성한다.
Hierachical Recurrent Attention Network(HRAN)
본 연구에서는 generation probability \(p(y_1,...,y_T\mid U)\)를 modeling하기 위해 HRAN을 제안한다.
아래 그림은 HRAN의 구조를 보여준다.
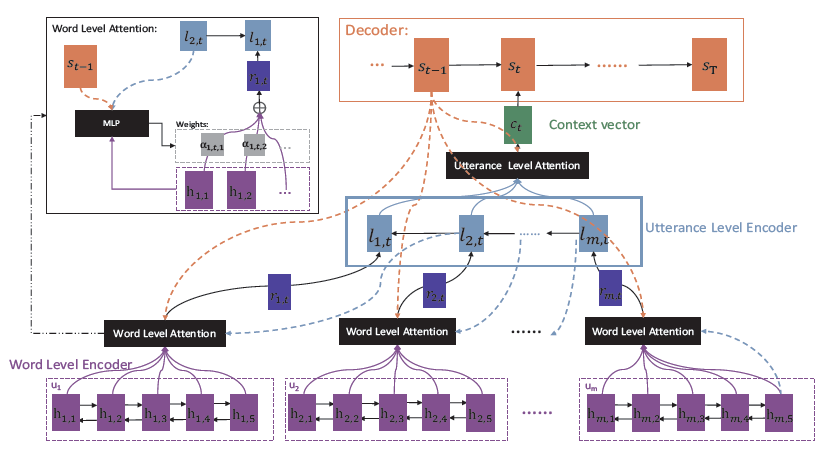
먼저, Word level의 encoder가 context의 모든 utterance들을 hidden vector로 encoding한다.
그 후, word를 생성할 때는, hierachical attention이 word level과 utterance level의 attention을 통해 utterance들 중에서 중요한 부분을 선택한다.
두 attention을 만들 때는 bottom up 방식으로 만들어진다.
먼저, utterance들의 hidden vector가 word level attention을 통해 만들어지고, 그 hidden vector들이 utterance level의 encoder에 전달되어 context의 hidden vector를 만든다.
Context의 hidden vector는 utterance level의 attention에 의해 처리되고, decoder로 전달되어 word를 생성한다.
과정을 순서대로 정리해보면 아래와 같다.
- Word level encoder가 모든 utterance들을 utterance hidden vector로 만들고, 이 때, word level attention을 사용한다.
- Utterance level encoder가 utterance hidden vector들을 전달받아 context hidden vector를 만들고, 이 때, utterance level attention을 사용한다.
- Decoder가 context hidden vector를 전달받아 word를 생성한다.
Word Level Encoder
\(U=(u_1,...,u_m)\)이 주어졌을 때, bidirectional GRU를 사용해 utterance \(u_i\)를 hidden vector \((h_{i,1},...,h_{i,T_i})\)로 encoding한다.
또한 \(k\in\{1,...,T_i\}\)에 대해서 \(h_{i,k}=concat(\overrightarrow{h}_{i,k},\overleftarrow{h}_{i,k})\)이고, \(\overrightarrow{h}_{i,k},\overleftarrow{h}_{i,k}\)는 각각 forward, backward 방향 GRU의 \(k\)번째 hidden state를 의미한다.
Forward GRU의 state \(\overrightarrow{h}_{i,0}\)은 isotropic Gaussian distribution으로 초기화된다.
Hierachical Attention and Utterance Encoder
Time step \(t\)에서 \(t-1\)개의 word를 만든 상태일 때, word level attention은 \(\{h_{i,j}\}_{j=1}^{T_i}\)에 대한 weight vector \((a_{i,t,1},...,a_{i,t,T_i})\)를 계산하고 utterance \(u_i\)를 vector \(r_{i,t}\)로 만든다.
\(\forall i\in \{1,...,m\}\)에 대해 \(r_{i,t}=\sum_{j=1}^{T_i}a_{i,t,j}h_{i,j}\)로 정의한다.
그 후에, utterance level encoder가 \(\{r_{i,t}\}_{i=1}^m\)를 input으로 받아 hidden vector \((l_{1,t},...,l_{m,t})\)를 만드는데, utterance level encoder는 backward로 encoding을 진행하며 GRU의 state \(l_{m+1,t}\)는 isotropic Gaussian distribution으로 초기화된다.
그 후, 아래와 같이 context vector \(c_t\)를 계산한다.
\[c_t=\sum_{i=1}^{m}\beta_{i,t}l_{i,t}\]여기서, \(\beta_{i,t}\)는 utterance level attention에 의해 \(l_{i,t}\)에 할당되는 weight이다.
Utterance vector \(r_{i,t}\)와 context vector \(c_t\) 를 만드는 과정 모두 아래 level에서 중요한 정보에 더 높은 weight를 부여해 vector를 만드는 것을 확인할 수 있다.
다시말하면, utterance vector를 만들 때는, 중요한 word에 높은 weight를 할당하고 context vector를 만들 때는, 중요한 utterance에 높은 weight를 할당한다.
이것이 두개의 hierachical attention이 작동하는 과정이다.
Word level attention은 일반적인 attention과는 다르게 decoder와 utterance level encoder의 hidden state에 dependency를 가진다.
Utterance level encoder가 backward로 진행되기 때문에 word level attention이 각 utterance를 처리하는 과정도 backward로 진행된다.
즉, \(m\)번째 utterance \(\{h_{m,j}\}_{j=1}^{T_m}\)를 먼저 처리하고 \(1\)번째 utterance \(\{h_{1,j}\}_{j=1}^{T_1}\)을 가장 나중에 처리하게 된다.
Word level attention이 하나의 utterance에서 각각의 word에 부여하는 가중치 \(a_{i,t,j}\)를 계산할 때, word level encoder의 hidden state인 \(h_{i,j}\) 뿐 아니라, 이전 time step \(t-1\) 시점에서 decoder의 hidden state인 \(s_{t-1}\)과 utterance level encoder의 \(i+1\)번째, 즉, 다음 utterance에 해당하는 hidden state \(l_{i+1,t}\)를 같이 사용한다.
각 가중치들은 아래와 같이 계산한다.
\[e_{i,t,j}=\eta(s_{t-1},l_{i+1,t},t_{i,j})\\ a_{i,t,j}=\frac{exp(e_{i,t,j})}{\sum_{k=1}^{T_i}exp(e_{i,t,k})}\]여기서, \(\eta\)는 MLP layer를 의미한다.
HRAN에서 word level attention과 utterance level encoder는 서로 dependent하다.
\(i\)번째 utterance의 각 word들의 가중치 \(a_{i,t,j}\)와 \(i+1\)번째 utterance에 해당하는 utterance level encoder의 hidden state인 \(l_{i+1,t}\) 사이에 dependency를 만든 것은 \(i+1\)번째 utterance의 내용이 그 이전 utterance인 \(i\)번째 utterance에서 어떤 word들이 중요한지의 정보를 가지고 있다는 가정에서 시작됐다.
또한 word level attention과 utterance level encoder가 backward 방향으로 처리하는 것은 context의 history를 역으로 비교하며 어떤 부분이 중요한지를 계산하기 위함이다.
\(\{l_{i,t}\}_{i=1}^m\)에 대해, utterance level attention은 아래와 같이 가중치를 계산한다.
\[e'_{i,t}=\eta(s_{t-1},l_{i,t})\\ \beta_{i,t}=\frac{exp(e'_{i,t})}{\sum_{i=1}^mexp(e'_{i,t})}\]Decoding the Response
HRAN의 decoder는 context vector \(\{c_t\}_{t=1}^T\)에 대한 conditional RNN language model이다.
Probability distribution \(p(y_1,...,y_T\mid U)\)는 아래와 같이 정의된다.
\[p(y_1,...,y_T\mid U)=p(y_1\mid c_1)\Pi_{t=2}^Tp(y_t\mid c_t,y_1,...,y_{t-1})\\ s_t=f(e_{y_{t-1}},s_{t-1},c_t)\\ p(y_t\mid c_t,y_1,...,y_{t-1})=\mathbb{I}_{y_t}\cdot softmax(s_t,e_{y_{t-1}})\]여기서, \(s_t\)는 time step \(t\)에서 decoder의 hidden state이고, \(e_{y_{t-1}}\)은 \(y_{t-1}\)의 embedding, \(f\)는 GRU, \(\mathbb{I}_{y_t}\)는 \(y_t\)의 one hot vector, 그리고 \(softmax(s_t,e_{y_{t-1}})\)은 vocabulary size의 vector이다.
\(\Theta\)를 HRAN의 parameter set이라고 할 때, 목적 함수는 아래와 같다.
\[\hat{\Theta}=argmin_\Theta-\sum_{i=1}^Nlog\,(p(y_{i,1},...,y_{i,T_i}\mid U_i))\]\(\hat{\Theta}\)는 dataset \(\mathbb{D}=\{(U_i,Y_i\}_{i=1}^N\)에 대한 estimator이다.
논문 링크
AAAI 2018
Hierarchical Recurrent Attention Network for Response Generation

Leave a comment